1483. 树节点的第 K 个祖先 - 力扣(LeetCode)
给定n=7, 每个元素的祖先[-1,0,0,1,1,2,2]
对应树为:
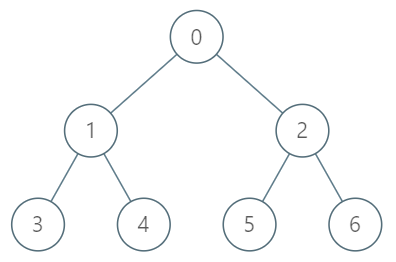
要求给定元素n,求出其第k个祖先
本题的主要思想是倍增。如果采用暴力解,求5的第10个祖先,要先求parent[5],再求parent[parent[5]]…以此类推,最终导致超时。
优化上述步骤,$k=10=(1010)_2=8+2$,即我们可以先求5的第二个祖先,再求该祖先的第10个祖先
创建数组$pa = n*m$,其中n为输入的元素个数,m为k(第k个祖先)的二进制位数。第i行j列表示第i个元素的第$2^j$个祖先。
*因为k<n,因此我们让m=n的二进制位数
- 第2个祖先=第1个祖先的第1个祖先
- 第4个祖先=第2个祖先的第2个祖先
- …
因此我们按列遍历,每次预处理所有元素的第$2^j$个祖先
class TreeAncestor {
private int[][] pa;
public TreeAncestor(int n, int[] parent) {
int m = 32 - Integer.numberOfLeadingZeros(n); // n 的二进制长度
pa = new int[n][m];
for(int i=0; i<n; i++) pa[i][0] = parent[i];
for(int j=0; j<m-1; j++){
for(int i=0; i<n; i++){
int p = pa[i][j];
pa[i][j+1] = p<0?-1:pa[p][j];
}
}
}
public int getKthAncestor(int node, int k) {
int m = 32 - Integer.numberOfLeadingZeros(k);
for(int i=0; i<m; i++){
if(((k>>i)&1)==1) node = pa[node][i];
if(node<0) break;
}
return node;
}
}